今日收获就是没有收获，跟风感谢日文和涛总的陪伴~

问题引入源自两方面：

1.老板提问：

为了对比ab两组流量的ctr差别，在给点显著性水平和期望误差1%内的条件下，可以计算出所需最小的样本量。随后根据流量顺序划分AB两组作为实验组和对照组。在该分组的基础上，评价使用核心指标变为gmv（每个人在周期内的总购买金额）。空跑4天，结果发现AB两组gmv差异已经存在，甚至有些时间区间上显著。如果仍坚持开始实验，如何通过数据分析的方法，说明最终结果差异显著是由于实验处理而不只是分组本身差异或者其他因素？

2.面试问题：

Simpson 悖论在第一次面字节时被问到了，当时懵了一会才意识过来~ Simpson 悖论（总体和部分表现出相反结论，比如男女录取率在总体和不同专业分层的结果之间矛盾）本质上属于内生性问题（解释变量和误差项存在相关关系），常见的原因是遗漏变量（比如男女比例差异）。这说明，有时是无法从相关性推导出因果关系的。

1.Rubin Causal Model

$Z_i$ 表示个体i是否接受处理， $Y_i$ 表示结果变量，则个体i的观测结果是：

Y_i = Z_iY_i(1) + (1-Z_i) Y_i(0)

1.1 Causal effect

不可观测的个体因果作用 (ICE)

ICE: individual Causal effect，个体i的因果作用 causal effect :
$ICE = Y_i(1) -Y_i(0)$
而实验中的个体要么接受处理，要么接受对照，我们只能观测 $Y_i(1)$ 或者 $Y_i(0)$ ，便无法计算其因果作用，这是因果推断的基本问题。
可识别的平均因果作用 (ACE)

ACE: average Causal effect，定义为个体因果作用的期望：
$ACE = E(ICE) = E(Y1 −Y0) = E(Y_1) - E(Y_0)$
其中 $Y_1$ 表示个体接受处理之后的潜在结果，其期望可以由所有个体都接受处理的潜在结果的均值来估计。 $Y_0$ 同理。

但是在实际中，我们不可能让所有的个体都接受处理。我们分配实验组和对照组，而当 Z 做随机化的前提下有 $E(Y_1) = E(Y|Z =1 ) ,E(Y_0) = E(Y|Z = 0)$ 。此时个体是否处理与潜在结果无关，总体的平均因果作用可识别（可识别表示因果作用可以用观测数据的分布唯一的表示）:

ACE (随机化试验下) = E(Y |Z = 1) − E(Y |Z= 0)

1.2 随机化试验的理想与现实

理想：可忽略的分配机制

随机化试验对于平均因果作用的识别起着至关重要的作用。在有协变量的随机化试验中，平均因果作用是可识别的要求：

Z⊥{Y(1),Y(0)} | X

即给定协变量X 后，处理的分配机制是完全随机化的，这被叫做“可忽略性”。这里引出了因果推断问题最重要的一步，就是对对照组和实验组的平衡进行检测。

现实：混杂偏倚

当协变量的分布在处理组和对照组均衡时，则我们在协变量取值的每一层，都能得到该层平均因果作用的相合估计。当协变量的分布在处理组和对照组均衡时，就会出现不同层结果不一致甚至截然相反的矛盾。为了消除协变量的分布在处理组与对照组之间的差异，最基础的方法就是：

1.3 Matching 与倾向得分

简单的想法就是从对照组中找到和处理组中比较“接近” 的个体进行匹配，这样得出的作用，可以近似平均因果作用，“接近”的标准是基于观测协变量的。如果观测协变量的维数较高，匹配就很难实现了。

此时可以使用倾向得分匹配。倾向得分 ( propensity score ) 定义为条件概率:
$p(Z = 1|X)$ ，不难看出可以用 logistic 回归算出倾向得分。随后可以根据它分层/加权，得到各层/总体加权平均因果效应的估计。

这里，用一个性别协变量不平衡导致的辛普森悖论作为例子：

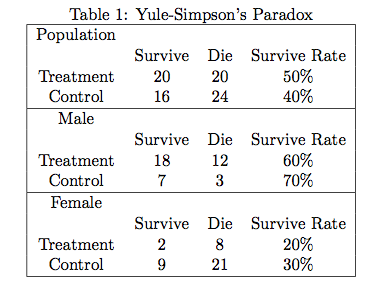
Y：结果变量，survive / die（则 E(Y) = P(Y=1) = survive rate ）
Z：随机分组变量，treatment / control
X：协变量，male / female
--
1.如果不考虑协变量性别的在分组中的不平衡问题，直接对男女总体进行估计：
ACE = E(y|z=1) - E(y|z=0) =  p(y=1|z=1) - p(y=1|z=0) = 0.5-0.4 = 0.1
-- 
2.如果考虑分组不平衡，按照协变量性别进行加权调整：
ACE = (p(y=1|z=1, x=1) - p(y=1|z=0, x=1))*p(x=1) + 
			(p(y=1|z=1, x=0) - p(y=1|z=0, x=0))*p(x=0) 
		= (0.6-0.7)*0.5 + (0.2-0.3)*0.5
		= -0.1
-- 
是否根据性别进行调整，得到的结果完全相反

2. 因果图 (Causal Diagram)

2.1 图模型基本概念

图模型的概念这部分在数据结构有所接触，这里回顾一下

其中重点在于DAG（有向无环图）/图模型/贝叶斯网络

在这张图中，x1...xj的联合分布可以根据全概率公式做如下的递归分解：

P(X_1, X_2, X_3, X_4, X_5, X_6, X_i, X_j) = P(X_1)(X_2)P(X_3|X_1) P(X_5|X_2)P(X_4| X_1, X_2)P(X_|X_3, X_4) P(X_6|X_i) P(X_j|X_4, X_5, X_6)

【注意点】一个有向无环图唯一地决定了一个联合分布；反过来，一个联合分布不能唯一地决定有向无环图（因为乘法公式的不唯一）

2.2 结构方程模型

structural equation model: SEM

SEM 是因果图的先驱。具体来说结构方程模型和图模型之间的关系：

原因Z——父节点，结果Y——子节点，间接原因X——Z的父节
外生变量：根节点
内生变量：子节点
边：函数关系

e.g. U = {X 教育程度，Y 经验} ， V = {Z 工资}

【注意点】因果关系&统计相关性：互相都不能推出另一方

2.3 V structure

不同结构下，如何快速判断条件独立性

链式结构（chain）

X 和 Z之间通过Y相连——则给定Y时，Z和X独立。condition 在哪儿相当于切断此处和周围的所有的连接。可以利用这个来解释辛普森悖论：

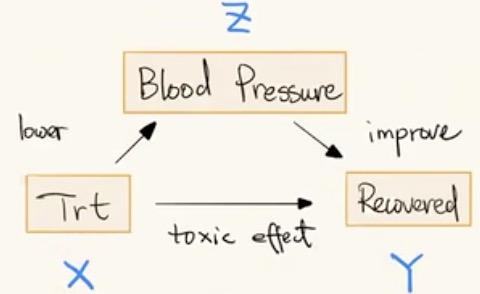
X是针对某一种疾病的药物，可以促进Y的恢复。具体来说，使用X可以帮助调节血压Z，从而促进Y的恢复。但当我们控制/condition on Z时，相当于切断此处的所有连接，只看X对Y的直接影响（副作用），结果则是抑制恢复。
叉状结构（fork）

X是的导致Y和Z的共同原因，Y 和 Z 是相关的——conditional在X上，Y和Z独立。可以利用这个来解释辛普森悖论：

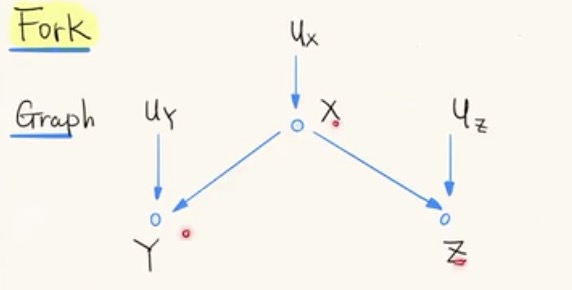
比如X：age，Y：exercie，Z：胆固醇含量。直接看Y和Z之间的关系，exercise 提高胆固醇含量增加。而加上 condition X 时，每个年龄段内 exercise 提高胆固醇含量降低。（why，年龄X对exercise Y 和胆固醇含量 Z 都有影响，年龄增加exercise 增多，胆固醇也增多）

另一个夸张的例子，穿着鞋睡觉和醒来头痛之间有强烈相关关系，而condition on 宿醉时，两者独立。

对撞结构（collider）

X 和 Y 是导致 Z 的共同原因。则 X 和 Y 独立，但当 condition 在 Z 或者 Z的后继节点上，则原本独立的 X 和 Y 变为相关。

比如智力和试题难度共同决定成绩高低，首先智力和难度是独立的，但当 condition 成绩时，两者出现相关。已知成绩低，如果智力高则说明试题难度高。已知成绩高，如果难度高说明智力也高。
d 分离 (d - separation)

定义（d 分离）: 设 $X$ ， $Y$ ， $Z$ 是 DAG 中不相交的节点集合， $\pi$ 为一条连接 $X$ 中某节点到 $Y$ 中某节点的路径（不管方向）。如果路径 $\pi$ 上某节点满足如下的条件：

（1）在路径 $\pi$ ， $w$ 点处为 $V$ 结构（或称冲撞点，collider），且 $w$ 及其后代不在 $Z$ 中；

（2）在路径 $\pi$ 上， $w$ 点处不是 $V$ 结构，且 $w$ 在 $Z$ 中,

那么称 $Z$ 阻断 (block) 了路径 $\pi$ 。进一步，如果 $Z$ 阻断了 $X$ 到 $Y$ 的所有路径，那么称 $Z$ d分离 $X$ 和 $Y$ ，记为 $(X\bot Y|Z)_{G}$ 。

如何直观理解d分离？用一个例子：

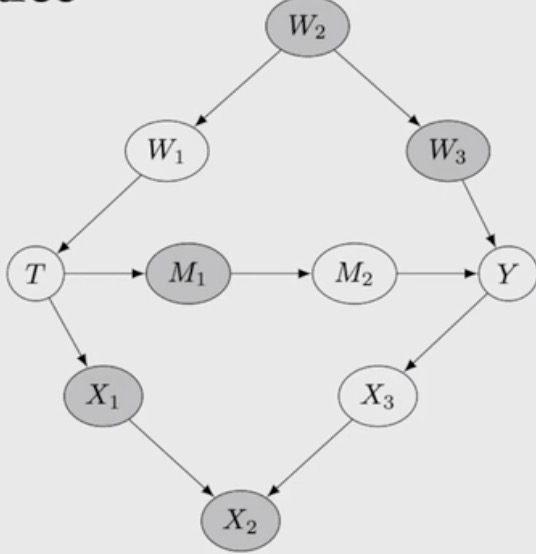
在这样的一个DAG中，观察到上方是 fork 结构，中间是 chain 结构，下方是 collider 结构。
找到能够 block 从 T 到 Y 所有路径的方式如下：
- M1 + W1/W2/W3（阻断fork&chain, collider 不动，对于（2）的情况）
- M1 + W1/W2/W3 + X2 + X1/X3（只有 X2 让下方的collider 父节点相关，加上X1或X3之后 T 和 Y 独立了。

2.4 从DAG到因果图

do-operator

“干预” vs “条件”

理解Do算子，从干预（intervening) 和条件 (conditioning) 的概念关系来理解。两个概念非常非常接近，在图模型中都相当于切断某处的所有连接，并且将其取值看做常数。但是区别在于，当我们引入“因果”的概念后，当我们干预“结果”，并不会影响“原因”的分布，但是当 condition on “结果”的时候，“原因”的条件分布会改变。

在上图的例子中，看条件和干预的区别：

A.条件 p(X1|x2)
- 无论X1和X2的因果关系如何，p(X1|X2)不变
B.干预 p(X1|do(X2))
- 在（1）的情况下，X1是原因X2是结果，则p(X1|do(X2)) = p(X1)【上面划线句】
- 在（2）的情况下，X1是结果X2是原因，则p(X1|do(X2)) = p(X1|X2)

backdoor / frontdoor criterion

。。。（没理解但是累了，so下周继续~

参考资料：

爱可可老师在B站上推荐的因果推理导论课

因果推断基本概念

1.Rubin Causal Model

1.1 Causal effect