第1题,两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那两个整数,并返回他们。假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍
- e.g. 给定 nums = [2, 7, 11, 15], target = 9,返回 [2, 7]
解法一:简单粗暴
for i 每一个数,计算和target的差值
def twoSum(nums, target):
notfound = True
i = 0
while i < len(nums) and notfound:
tmp = target - nums[i]
j = i+1
while j <len(nums) and notfound:
if nums[j] == tmp:
notfound = False
j += 1
i += 1
if not notfound:
return [i-1, j-1]
# 测试
twoSum(nums = [2,7,11,15,4], target = 9)
twoSum(nums = [2,7,11,15,4], target = 22)
twoSum(nums = [2,7,11,15,4], target = 8)
twoSum(nums = [2,7,11,15,4], target = 14)
twoSum(nums = [2,2,11,15,4], target = 4)
[0, 1]
[1, 3]
[0, 1]
解法二:转化成字典加快查找
def twoSum(nums, target):
d = {}
n = len(nums)
for i in range(n): # 转化成字典
d[nums[i]] = i # 如果有相同的字符,value变成最后一次出现时候的index
for i in range(n):
tmp = target - nums[i]
j = d.get(tmp) # 用字典查找
if (not j == None) and (not i==j): # 排除是本身
return [i,j]
# 测试
twoSum(nums = [2,7,11,15,4], target = 9)
twoSum(nums = [2,7,11,15,4], target = 22)
twoSum(nums = [2,7,11,15,4], target = 8)
twoSum(nums = [2,7,11,15,4], target = 14)
twoSum(nums = [2,2,11,15,4], target = 4)
[0, 1]
[1, 3]
[0, 1]
第20题,有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 空字符串可被认为是有效字符串。
解法一、做一个循环不断删除成对符号
迭代删掉成对的括号,虽然可以,但是复杂度高了
def isValid(strings): # leetcode上复杂度rank倒数
while len(list(strings))>1:
before = len(list(strings))
strings = strings.replace("()","").replace("[]","").replace("{}","")
after = len(list(strings))
if before == after:
break
if len(list(strings))==0:
return True
else:
return False
isValid("([]{{}})[{}[[]]]")
isValid("")
isValid("([)")
True
True
False
解法二、用一个栈来记录(标准)
- 从左边开始发现了左括号,push进去
- 发现了右括号,把栈尾部的pop出来对比,如果栈是空的——F,如果pop出来的不匹配——F,否则继续进行
- 最后看栈是不是空的
- 执行时间超过97%的
def isValid(strings):
string = list(strings)
left = ["(", "[", "{"]
right = [")", "]", "}"]
stack = []
for i in range(len(string)):
if string[i] in left:
stack.append(string[i])
if string[i] in right:
if len(stack)==0:
return False # 右括号多了
else:
tmp = stack.pop()
if left.index(tmp)!=right.index(string[i]): # 左右不匹配
return False
if len(stack)==0:
return True
else:
return False # 左括号多了
isValid("([]{{}})[{}[[]]]")
isValid("")
isValid("([)")
True
True
False
第21题,合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
思路——递归
- 结束条件:两个链表剩下的空了
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
a1 = ListNode(1)
a2 = ListNode(2)
a3 = ListNode(4)
a1.next = a2
a2.next = a3
b1 = ListNode(1)
b2 = ListNode(3)
b3 = ListNode(4)
b1.next = b2
b2.next = b3
def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode: # 要连接的下一个是什么
if not l1: return l2 # l1没有了,l2后面的直接接上
if not l2: return l1 # l2没有了,l1后面的直接接上
if l1.val <= l2.val: # 如果l1比l2小
l1.next = mergeTwoLists(l1.next,l2) # 用l1的下一个和l2比较,比较的结果作为1.next
return l1 # return l1 l2两者更小的(作为连接的next)
else:
l2.next = mergeTwoLists(l1,l2.next)
return l2
# 测试
mergeTwoLists(a1, b1)
a = a1
while a!=None:
print(a.val, end = " -> ")
a = a.next
<__main__.ListNode at 0x1044be8d0>
1 -> 1 -> 2 -> 3 -> 4 -> 4 ->
第53题,最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
解法一,简单粗暴
- 第一个数作为起点,如果直到下一个正数, sum_tmp <0,则记max[i] ==0 ,sum_tmp = 再次开始计算, 。
- 如果直到下一个正数 max > 0,则把max单独拿出来,如果max_next,如果max_next<0,则maxx=max,max=0
- 如果max_next>0,max=max+max_next
面试这样写会被打的,把问题复杂化了。。。,但是执行时间和内存消耗都挺小。。。
def max_Sum(nums):
maxsum = nums[0]
tmp_sum = nums[0]
for i in range(1,len(nums)):
if nums[i] > 0:
if tmp_sum <= 0:
tmp_sum = nums[i]
if tmp_sum > maxsum:
maxsum = tmp_sum
elif tmp_sum > 0:
tmp_sum = tmp_sum+nums[i]
maxsum = max(maxsum, tmp_sum)
elif nums[i] <= 0:
if maxsum<= 0:
maxsum = max(maxsum, nums[i])
elif maxsum> 0:
tmp_sum = tmp_sum + nums[i]
print(i, nums[i], tmp_sum, maxsum)
return(maxsum)
max_Sum( [-2,1,-3,4,-1,2,1,-5,4])
max_Sum( [-1,0])
1 1 1 1
2 -3 -2 1
3 4 4 4
4 -1 3 4
5 2 5 5
6 1 6 6
7 -5 1 6
8 4 5 6
6
1 0 -1 0
0
解法二,动态规划,超简洁
超简洁代码!
- nums在更新前是原始数据,从第二项开始往右更新,更新后记录子序和
- 每当当前数据比累计子序和要大时,重新从当前开始计算子序和。
nums = [-2,1,-3, 4, -1,2,1,-5,4]
for i in range(1,len(nums)):
nums[i] = max(nums[i-1]+nums[i], nums[i])
#print(nums)
max(nums)
[-2, 1, -3, 4, -1, 2, 1, -5, 4]
[-2, 1, -2, 4, -1, 2, 1, -5, 4]
[-2, 1, -2, 4, -1, 2, 1, -5, 4]
[-2, 1, -2, 4, 3, 2, 1, -5, 4]
[-2, 1, -2, 4, 3, 5, 1, -5, 4]
[-2, 1, -2, 4, 3, 5, 6, -5, 4]
[-2, 1, -2, 4, 3, 5, 6, 1, 4]
[-2, 1, -2, 4, 3, 5, 6, 1, 5]
6
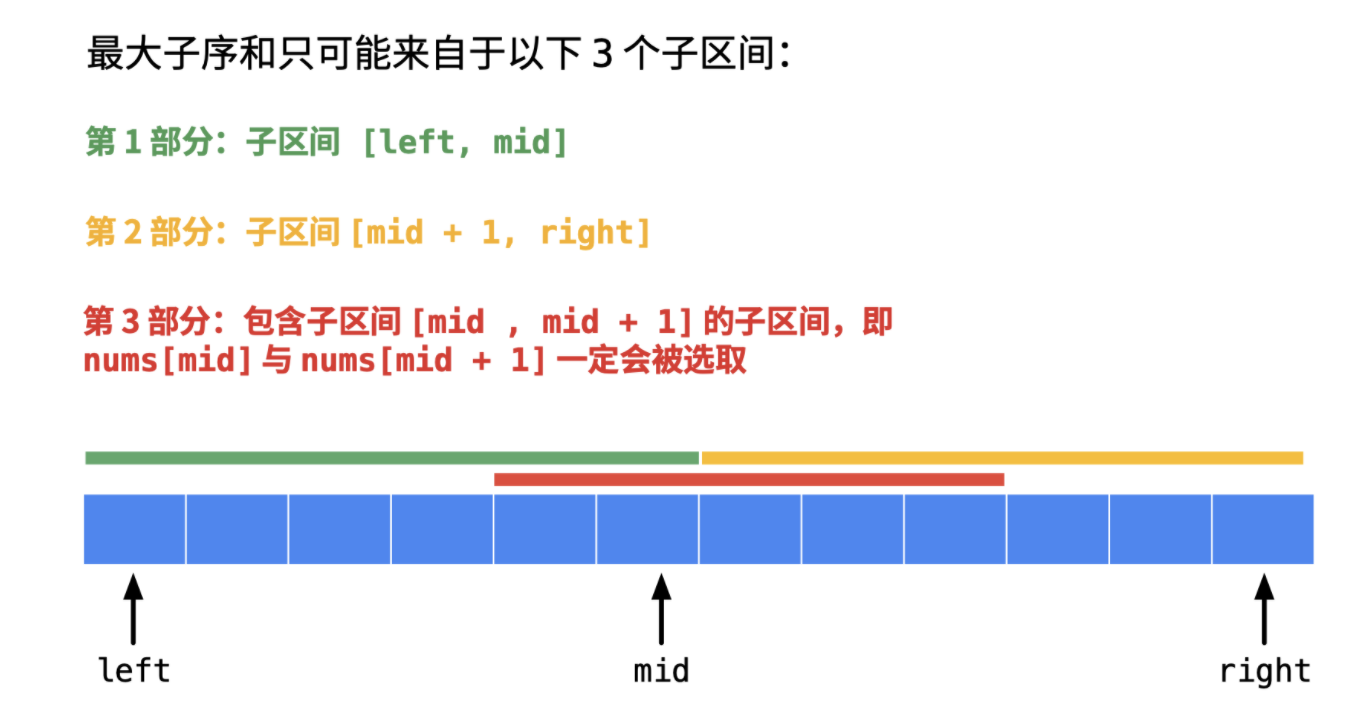
解法三,分治法
第70题,爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入: 3
输出: 3
解法一,简单粗暴,典型的递归问题
好蠢,超时了。。。
def climbStairs(n):
if n<=1: return 1
if n>1:
return(climbStairs(n-1)+climbStairs(n-2))
climbStairs(38)
63245986
解法二,优化递归
用一个字典记录,极大提升速度,但是内存消耗上去了(事实上不要保存之前的内容,可以考虑优化)
def climbStairs(n):
dict0 = {}
dict0[1] = 1
dict0[2] = 2
for n in range(3, n+1): # 这道题事实上是斐波那契数列——前两项求和
dict0[n] = dict0[n-1]+dict0[n-2]
#print(dict0)
return dict0[n]
climbStairs(38)
{1: 1, 2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986}
63245986