薅羊毛记录仪

旧岁舍人如木落 新春予义再易风

文章目录 站点概览

shuyi

83 文章
11 分类
11 标签

手动实现——SVM（线性可分问题）

发布于 2020-10-21 | 分类于 机器学习 | 11分钟 | 2192字数 | 浏览量：

SVM——完全线性可分问题

SVM原理 & 思路

  • 原理，具体见笔记本第19-29页

原理关键点

  1. 线性可分：能够找到超平面使得

$ y_i(w^T X_i +b ) \geq 1 $

  1. 原问题和对偶问题

    原问题：min12∣∣w∣∣2min \frac{1}{2} ||w||^2 限制条件为$ y_i(w^T X_i +b ) \geq 1$

    对偶问题：max⁡αmin⁡w,bL(w,b,α)\max \limits_{\alpha} \min\limits_{w,b}L(w,b,\alpha)

  2. 问题转化为极大化 $\theta(\alpha) $:

θ(α)=min⁡w,bL(w,b,α)=∑iαi−12∑i∑jαiαjyiyj(xi⋅xj)\theta(\alpha) = \min\limits_{w,b}L(w,b,\alpha) = \sum \limits_i \alpha_i - \frac{1}{2} \sum \limits_i\sum \limits_j \alpha_i \alpha_j y_i y_j (x_i\cdot x_j)

限制条件 :
{αi≥0∑αiyi=0\left\{\begin{matrix} \alpha_i \geq 0 & & \\ \sum \alpha_i y_i = 0& & \end{matrix}\right.

思路

  1. 利用SMO算法（序列最小最优化问题）计算αi\alpha_i

  2. 预测
    wTXi+b≥0,then1,wTXi+b<0,then−1w^T X_i +b\geq 0, then 1, w^T X_i +b < 0, then-1

  3. 可视化，希望画出分割线、margin、支持向量

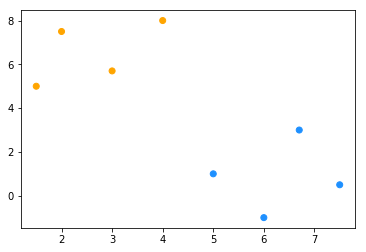
数据集

import numpy as np
import matplotlib.pyplot as plt

## 将代码块运行结果全部输出，而不是只输出最后的，适用于全文
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"    

## 造数据——一个线性可分的数据集
data_x = np.array([[1.5, 5], [2, 7.5], [3, 5.7], [4, 8], [5, 1], [6, -1], [6.7, 3], [7.5, 0.5]])
x1 = [data_x[i][0] for i in range(data_x.shape[0])]
x2 = [data_x[i][1] for i in range(data_x.shape[0])]
data_y = np.array([[1] * 4 + [-1] * 4]).T
color = ["orange" if c==1 else "dodgerblue" for c in data_y] 
fig = plt.figure(figsize=(6, 4))   # 创建一张画布
plt.scatter(x1, x2, c = color)

SMO算法

利用SMO算法（序列最小最优化问题）计算αi\alpha_i，参考资料快速理解SMO算法

why SMO?

  1. 参数很多——梯度下降（每次对所有参数更新）复杂度太高；由于约束条件的存在，每次调整两个参数，把问题转化为一系列子问题。

  2. 假定其他alpha固定，只更新α1α2\alpha_1 \alpha_2，根据约束条件α2\alpha_2可以表示为α1\alpha_1的函数，优化问题可以有解析解（不用搜索直接计算，其实就是一个一元二次函数求极值的问题，但是要注意极值点是不是在取值的约束内）——速度提升

思路

  1. 参数初始化（0）
  2. 选取两个参数进行优化（其中至少有一个是违背kkt条件的）计算最优解，看最优解是否在取值范围内（剪辑），然后更新参数，并计算更新后的b和Ei
  3. 是否满足停止算法条件（达到迭代次数/参数更新量太小），如果不满足就再次选取两个参数（记录迭代次数）

辅助函数

  1. 计算预测值
    $Ei = \sum \alphayk +b $

  2. 根据取值范围剪辑alpha，看最优解是否在取值范围内（剪辑）

  3. KKT条件

根据强对偶定理有alpha=0或者Ei=0

  1. 计算eta 方便后续更新alpha值

  2. 计算取值范围上下界

  3. 计算b bjnew=yj−∑αiyikijb_j^{new} = yj - \sum \alpha_i y_i k_{ij}

  4. 选出第一个变量后随机选择第二个

### 1.计算预测值
def count_Ei(alphas, b, x, xi, y, yi):    
    '''
    输入的维度：alphas(n,1), b(1,1),x(n,p),xi(1,p),y(n,1)
    '''
    # 计算xi和其他xj的内积——输出向量(k1i,k2i,...kni)
    ki = np.sum(x*xi, axis = 1) 
    # 计算预测值
    resulti = ki@(alphas*y)+b-yi
    return resulti


### 2.根据取值范围剪辑alpha
def clipAlpha(alpha,L,H):
    if alpha > H: 
        alpha = H
    if L > alpha:
        alpha = L
    return alpha


### 3.定义KKT条件
def match_kkt(alphai, Ei):
    '''
    输入两个数字，根据强对偶定理有alpha=0或者Ei=0
    '''
    return ((alphai==0) and (Ei > 1 or Ei < -1)) or ((alphai>0) and (Ei==0))
 
    
### 4.计算η
def count_eta(xi, xj):
    etaij = xi.T@xi + xj.T@xj - 2*xi.T@xj
    return etaij


### 5.计算取值范围上下界
def alpha_LH(alphai, alphaj, yi, yj):
    '''
    alphaj是更新对象的old值，alphai是另一个对象的old值
    '''
    if yi==yj:
        Lij = 0
        Hij = max(0, alphai + alphaj)
    else:
        Lij = max(0, alphaj- alphai)
        Hij = 99999      
    return Lij, Hij

### 6.计算b更新后的值
def count_b(alphas, x, y, xj, yj):
    '''
    输入自变量因变量xy，准备用第j个alpha计算b——需要xj和yj
    '''
    bj_new = yj - np.sum(x*xj, axis = 1)@(alphas*y)
    return bj_new.tolist()

### 7. 随机选择第二个变量
import random
def selectJrand(i,m):
    j=i 
    while (j==i):
        j = int(random.uniform(0,m))
    return j

# 测试
alphas = np.zeros((data_x.shape[0], 1))
count_Ei(alphas = alphas, b=0, x = data_x, xi = data_x[0], y= data_y, yi = data_y[0])
match_kkt(alphai=0, Ei=1)
count_eta(data_x[0], data_x[1])
count_b(alphas, data_x, data_y, data_x[0], data_y[0])
selectJrand(0,8)

array([-1.])

False

6.5

[1.0]

2

正式编写

参考统计学习方法（李航）第128-130页

  1. 第一步，取出两个alpha

    • 首先for每一个i，（根据当前参数值）计算Ei —>
    • 判断alphai是否满足kkt条件，如果遇到不满足的就作为第一个变量 —>
    • 在剩下的里面找一个j作为第二个变量

  2. 第二步，

    • 计算alpha j 的最优解=αjold+yj(Ei−Ej)/η=\alpha_j^{old}+y_j(Ei-Ej)/\eta、取值范围，再做剪辑，更新alpha j
    • 如果发现alpha j更新量很少——回到第一步，重新选择两个alpha
    • else就根据alpha j计算alpha i的值（根据kkt条件等式约束）

    αiyi+αjyj=−∑k!=i,jαkyk\alpha_i y_i + \alpha_j y_j = -\sum_{k!=i,j} \alpha_k yk

    • 更新之后再次计算b 更新b的值
    • 记录迭代更新次数

  3. 迭代循环上述步骤，限制条件是迭代次数<最大值

# 参数初始化：
n = data_x.shape[0]
alphas = np.zeros((n, 1))
b = 0
iteration=0

while(iteration<=3):
    change = False
    for i in range(n):
        #####   第一步   #####
        # 寻找一个不满足kkt条件的ai
        # 计算Ei，用来判断kkt条件
        Ei = count_Ei(alphas = alphas, b = b, x = data_x, xi = data_x[i], y= data_y, yi = data_y[i])
        if not match_kkt(alphas[i], Ei):    # 如果不满足kkt条件，则继续
            # 从剩下的里面随机选择j
            j = selectJrand(i, n)
            alphaj_old = alphas[j].copy()   # 记录j更新前的数值
            alphai_old = alphas[i].copy() 
            
            #####   第二步   #####
            # 更新alphai alphaj
            alphaj_LH = alpha_LH(alphas[i], alphas[j], data_y[i], data_y[j])  # 计算取值范围
           # if alphaj_LH[0]==alphaj_LH[1]: continue
            Ej = count_Ei(alphas = alphas, b = b, x = data_x, xi = data_x[j], y=data_y,yi = data_y[j])  # 计算Ej
            etaj = count_eta(data_x[i],data_x[j])   # 计算eta
            #if etaj > 0: continue
            alphaj_new = alphaj_old + data_y[j]*(Ei-Ej)/etaj  #计算alphaj最优解
            alphaj_new = clipAlpha(alphaj_new,L = alphaj_LH[0], H = alphaj_LH[1])  # 做剪辑
            # 如果发现更新量大于0.001，后续不用进行
            if (abs(alphaj_new-alphaj_old)<0.001): continue   # 跳出本次循环
            change = True
            alphas[j] = alphaj_new
            
            # 再根据alphaj的值计算alphai
            alphai_new = alphai_old + data_y[i]* data_y[j]*(alphaj_old-alphaj_new)
            alphas[i]  = alphai_new
            
             #####   第三步   #####
            # 更新b
            bi = b-Ei-data_y[i]*(data_x[i]@data_x[i])*(alphai_new-alphai_old)-data_y[j]*(data_x[i]@data_x[j])*(alphaj_new-alphaj_old)
            bj = b-Ej-data_y[i]*(data_x[i]@data_x[j])*(alphai_new-alphai_old)-data_y[j]*(data_x[j]@data_x[j])*(alphaj_new-alphaj_old)
            b = (bi + bj)/2
    if change: iteration = iteration+1
    iteration

### 结果
alphas,b

1

2

3

4   

 (array([[0.        ],
        [0.        ],
        [0.09610824],
        [0.        ],
        [0.0115309 ],
        [0.        ],
        [0.08457734],
        [0.        ]]), array([0.39743575]))

模型拟合&预测

### 定义预测函数
def SVM_pred(train_x, train_y, test_x, alphas, b):
    test_pred = []
    test_decision = []
    for i in range(len(test_x)):
        tmp = np.sum(train_x*test_x[i], axis = 1) @(alphas * train_y) + b
        test_pred.append(tmp)
        if tmp >= 0 :
            tmp = 1
        if tmp < 0 :
            tmp = -1
        test_decision.append(tmp)
    return test_pred,test_decision

# 对于训练集上的拟合值
train_pred, train_decision = SVM_pred(data_x,data_y,data_x,alphas,b)
train_pred

[array([1.3062091]),
 array([1.84459527]),
 array([1.]),
 array([1.31387637]),
 array([-1.]),
 array([-1.90110608]),
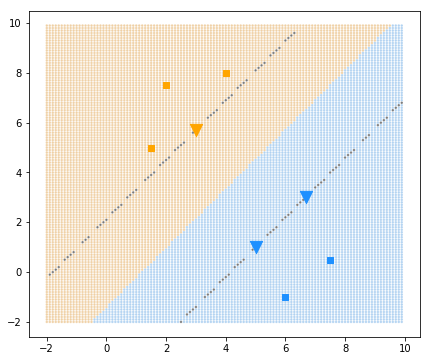
 array([-1.00608842]),
 array([-1.98127194])]

根据拟合结果可以看出

样本3和样本5、7 为支持向量，接下来考虑可视化

可视化

  1. 分类界限：用测试数据的背景点表示
  2. 支持向量：用三角形表示
  3. margin：通过测试数据画出来
xx1, xx2 = np.meshgrid(np.arange(-2, 10, 0.1), np.arange(-2, 10, 0.1))   # 生成自变量的数据
test_xx = [[xx1.ravel()[i],xx2.ravel()[i]] for i in range(len(xx1.ravel()))]
yy_pred,yy_decision = SVM_pred(data_x,data_y,test_xx, alphas, b)

fig = plt.figure(figsize=(7, 6))   # 创建一张画布
# 背景网格点
color = ["#e2a653" if c==1 else "#6cabe6" for c in yy_decision] 
for i in range(len(yy_pred)):
    if abs(abs(yy_pred[i])-1)<0.01:
        color[i] = "black"

plt.scatter(xx1, xx2, c = color, alpha = 0.35, marker= ".",s = 10)
# 原始数据的点
color = ["orange" if c==1 else "dodgerblue" for c in data_y] 
markers = ["v" if abs((abs(m)-1))<0.01 else "s" for m in train_pred]
size = [150 if abs((abs(m)-1))<0.01 else 30 for m in train_pred]
[plt.scatter(x1[i], x2[i], c = color[i], marker = markers[i], s =size[i]) for i in range(len(color))]
# 机器学习
练习题 DAY1 上一篇
【系列】leetcode笔记 下一篇
Powered by Gridea | © 2019-2020 Theme By HsxyHao
学习笔记 & 日常生活