1.通用的深度优先搜索

vertex增加两个属性

discovery 发现时间，第几步访问到并被设置为灰色
finish 结束时间，第几步结束探索并被设置为黑色

graph 增加一个属性

time 记录算法执行的步骤

方法：类的继承 super

class DFSGraph(Graph): 
    def __init__(self):
        super().__init__()   # 继承graph里init里的属性
        self.time = 0        # 新增属性 time
    
    def dfs(self):
        for aVertex in self:
            aVertex.setColor('white')
            aVertex.setPred(-1)   # 设置前驱顶点
        for aVertex in self:
            if aVertex.color=="white":
                self.dfsvisit(aVertex)   # 递归调用
    
    def dfsvisit(self, startVertex):
        # 开始探索
        startVertex.setColor("grey")  
        self.time += 1
        startVertex.setDiscovery(self.time)    # 记录开始的时间
        for nextVertex in startVertex.getConnections():
            if nextVertex.color=="white":     # 对于没有发现过的新顶点
                nextVertex.setPred(startVertex)  # 设置前驱
                self.dfsvisit(nextVertex)        # 递归调用
        
        # 结束探索
        startVertex.setColor('black')
        self.time += 1
        startVertex.setFinish(self.time)     # 记录结束时间

2.拓扑排序

从“工作流程图”到“工作次序排列”的算法

图建立：
- 工作项——节点；工作流程——图
- 一个DAG（有向无圈图【否则循环依赖】），输出顶点的线性序列
- 要求存在边(v,w)，则线性序列中v在w之前
实现——深度优先搜索DFS
- 调用

3.强连通分支

发现高度聚集节点群

图G的子集C，任意两个顶点之间都有路径来回——C是具有这样性质的最大子集
找到之后可以对顶点分类合并——简化

图的转置

图的转置代表把图所有有向边的顶点交换次序——图和转置图的强连通分支没有变

Kosaraju 算法

首先调用通用DFS计算结束时间
对图进行转置，再调用DFS计算，每个顶点的搜索循环按照上一步计算的结束时间倒序来搜索
生成深度优先森林，每一棵树都是一个强连通分支

4.最短路径问题（带权重）

例子：路由器连接的网络，负责把信息传递，终端试试“traceroute www....”

顶点：路由器；边：网络连接；权重：速度、负载程度、优先级等等因素抽象为权重
权重越高，代价越高，希望找到代价最小的路径

DIJKSTRA

一个确定的开始节点到所有图中其他节点的最短路径

顶点Vertex类中使用dist 作为实例变量，包含从起点到目的节点的最小权值路线的当前总权值。
各顶点先后顺序是由一个优先队列控制的，队列中决定顺序的参量是dist值，初始dist尽可能的大
每次最低dist的顶点优先pop出来，计算权重会引起dist的减小——重排
重复上述，每一个节点，算法均会重复一次

from pythonds import PriorityQueue, Graph, Vertex

# 最短路径
# G - 无向赋权图
# start - 开始节点
# 返回从开始节点到其它所有节点的最短带权路径
def dijkstra(G, start):
    pq = PriorityQueue()  # 创建优先队列
    start.setDistance(0)  # 起点距离设置为0，其它节点距离默认maxsize
    # 将节点排入优先队列，start在最前面
    pq.buildHeap([(v.getDistance(), v) for v in G])
    while not pq.isEmpty():
        # 取从start开始距离最小的节点出队列，作为当前节点
        # 当前节点已解出最短路径
        currentVert = pq.delMin()
        # 遍历节点的所有邻接节点
        for nextVert in currentVert.getConnections():
            # 从当前节点出发，逐个加上邻接节点的距离进行检验
            newDist = currentVert.getDistance() \
                      + currentVert.getWeight(nextVert)
            # 如果小于邻接节点原有距离，就更新邻接节点
            #print("{}，原距离 = {}，新距离 = {}".format(nextVert.getId(), newDist, nextVert.getDistance()))
            if newDist < nextVert.getDistance():
                # 更新距离值
                nextVert.setDistance(newDist)
                # 更新返回路径
                nextVert.setPred(currentVert)
                # 更新优先队列
                pq.decreaseKey(nextVert, newDist)

                
G = Graph()
ndedge = [('u', 'v', 2), ('u', 'w', 5), ('u', 'x', 1),  # 边和权重
          ('v', 'x', 2), ('v', 'w', 3), ('x', 'w', 3),
          ('x', 'y', 1), ('w', 'y', 1), ('w', 'z', 5),
          ('y', 'z', 1)]
for nd in ndedge:
    G.addEdge(nd[0], nd[1], nd[2])
    G.addEdge(nd[1], nd[0], nd[2])
start = G.getVertex('u')       # 从u开始
dijkstra(G, start)                # 计算从u开始最短路径的权重和

for i in G.getVertices():
    print(G.getVertex(i))

u:color white:disc 0:fin 0:dist 0:pred 
	[None]

v:color white:disc 0:fin 0:dist 2:pred 
	[u:color white:disc 0:fin 0:dist 0:pred 
	[None]
]

w:color white:disc 0:fin 0:dist 3:pred 
	[y:color white:disc 0:fin 0:dist 2:pred 
	[x:color white:disc 0:fin 0:dist 1:pred 
	[u:color white:disc 0:fin 0:dist 0:pred 
	[None]
]
]
]

x:color white:disc 0:fin 0:dist 1:pred 
	[u:color white:disc 0:fin 0:dist 0:pred 
	[None]
]

y:color white:disc 0:fin 0:dist 2:pred 
	[x:color white:disc 0:fin 0:dist 1:pred 
	[u:color white:disc 0:fin 0:dist 0:pred 
	[None]
]
]

z:color white:disc 0:fin 0:dist 3:pred 
	[y:color white:disc 0:fin 0:dist 2:pred 
	[x:color white:disc 0:fin 0:dist 1:pred 
	[u:color white:disc 0:fin 0:dist 0:pred 
	[None]
]
]
]

5.最小生成树

信息广播问题，希望覆盖到所有顶点，同时总费用最少

含义

生成树：拥有图中所有的顶点和最少的边，仍然保持连通的子图
最小生成树：包含图G(v,e)的所有顶点v和E的无圈子集，并且边权重和最小。

Prim

贪心算法 每一步都沿着权重最小的边前进搜索，如果还不是生成树则——添加一条最小权重的可以安全添加的边
可以安全添加的边：

from pythonds import PriorityQueue, Graph, Vertex
 
# 最小生成树prim算法
# G - 无向赋权图
# start - 开始节点
# 返回从开始节点创建最小生成树
def prim(G, start):
    pq = PriorityQueue()  # 创建优先队列
    start.setDistance(0)  # 起点最小权重代价设置为0，其它节点最小权重代价默认maxsize
    # 将节点排入优先队列，start在最前面
    pq.buildHeap([(v.getDistance(), v) for v in G])
    while not pq.isEmpty():
        # 取距离*已有树*最小权重代价的节点出队列，作为当前节点
        # 当前节点已解出最小生成树的前驱pred和对应最小权重代价dist
        currentVert = pq.delMin()
        # 遍历节点的所有邻接节点
        for nextVert in currentVert.getConnections():
            # 从当前节点出发，逐个检验到邻接节点的权重
            newCost = currentVert.getWeight(nextVert)
            print((nextVert.id), end = " ")
            # 如果邻接节点是"安全边"，并且小于邻接节点原有最小权重代价dist，就更新邻接节点
            if nextVert in pq and newCost < nextVert.getDistance():
                # 更新最小权重代价dist
                nextVert.setPred(currentVert)
                # 更新返回路径
                nextVert.setDistance(newCost)
                # 更新优先队列
                pq.decreaseKey(nextVert, newCost)
                print((nextVert.id, newCost))

G = Graph()
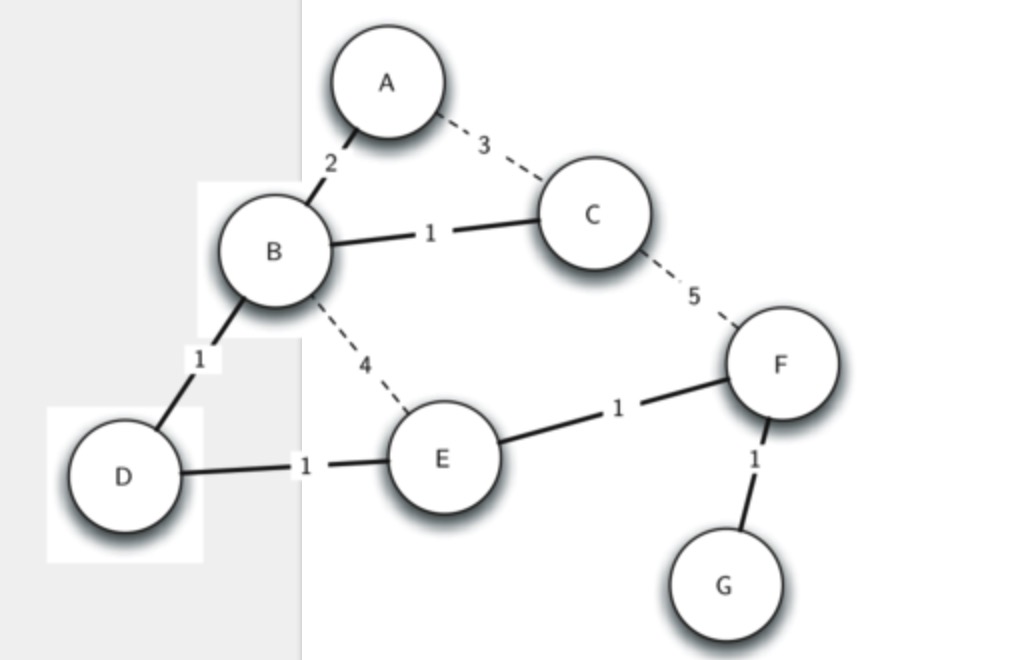
ndedge = [('A', 'B', 2), ('A', 'C', 3), ('B', 'C', 1),
          ('B', 'D', 1), ('B', 'E', 4), ('C', 'F', 5),
          ('D', 'E', 1), ('E', 'F', 1), ('F', 'G', 1)]
for nd in ndedge:
    G.addEdge(nd[0], nd[1], nd[2])
    G.addEdge(nd[1], nd[0], nd[2])
start = G.getVertex('A')
prim(G, start)

B ('B', 2)
C ('C', 3)
A C ('C', 1)
D ('D', 1)
E ('E', 4)
A B F ('F', 5)
B E ('E', 1)
B D F ('F', 1)
C E G ('G', 1)
F

图——其他算法

1.通用的深度优先搜索

2.拓扑排序

3.强连通分支

图的转置

Kosaraju 算法

4.最短路径问题（带权重）

DIJKSTRA

5.最小生成树

含义

Prim

感谢您的支持，我会继续努力的!