手动实现——Logistic与Roc曲线

思路：

读入数据&预处理&分训练集和预测集
定义函数——计算交叉熵损失coss、w和b的偏导
定义函数——迭代梯度下降
预测混淆矩阵 & ROC曲线 & 可视化分类边界

数据预处理

import os
#import random     
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

## 将代码块运行结果全部输出，而不是只输出最后的，适用于全文
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"    

# font_manager函数，用于指定中文字体样式、大小
import matplotlib.font_manager as mfm
font_path = r"/Users/mac/Library/Fonts/字体管家方萌简（非商业使用）v1.1.ttf"
prop = mfm.FontProperties(fname = font_path)

## 读入数据
os.chdir("/Users/mac/Desktop/快乐研一/python/机器学习python实现")
dating = pd.read_csv("Speed Dating Data.csv", encoding = "gbk")

## 提取变量——是否接受dec（因变量0-1）、好感度like、吸引力attr
dating = dating[['like','attr','dec']]
dating.head()

## 缺失问题
dating.isnull().sum(axis=0)  # 缺失比例
dating.dropna(axis = 0, how='any', thresh = None, subset = None, inplace=True)   # omit na值
print("去掉缺失之后总样本量{}".format(len(dating)))

## 分为训练集和测试集
sample = np.random.choice(range(len(dating)), int(len(dating)*0.8), replace= False).tolist()
dating_train = dating.iloc[sample, :]
dating_test = dating.iloc[[x for x in range(len(dating)) if x not in sample], :]
print("训练集样本量 = {}, 测试集样本量 = {}".format(len(dating_train),len(dating_test)))

去掉缺失之后总样本量8122
训练集样本量 = 6497, 测试集样本量 = 1625

定义函数——计算交叉熵的cost&梯度

输入：x,y,w,b
计算yhat（最好先定义一个sigmoid方便计算）、coss、对于w和b的梯度
输出：yhat/coss/dw/db

这里就按照向量计算来，假定w是(p,1)维的向量，b是常数，数据(n,p)，y和y_hat是(n,1)维的向量

矩阵/向量的乘法：np.dot

# 前置知识——py中的矩阵运算：
'''
a = np.zeros((3,2));b = a+1;c = a+2
b
b.T   # 矩阵转置
b*c  # 每一项相乘
b+c  # 每一项相加
np.dot(b.T,c)   # 真正的矩阵乘法
np.sum(c)       # 每一项的总和
'''

# 定义sigmoid函数
def sigmoid(x):           
    z = 1/(1+np.exp(-x))
    return z

# 定义函数计算梯度
def logistic(X,y,w,b):      # 计算当前梯度
    # 根据输入的w和b，计算yhat，再加上x和y计算并输出梯度
    yhat = sigmoid(np.dot(X, w) + b)     # 计算预测值
    cost = (-1/len(X)) *(int(np.dot(y.T,np.log(yhat)))+np.dot((1-y.T), np.log(1-yhat)))   # 计算交叉熵
    dw = np.dot(X.T, np.squeeze(yhat)-y)/len(X)   # 计算梯度
    db = np.sum(np.squeeze(yhat)-y)/len(X)        # 计算梯度
    return np.squeeze(yhat), cost, dw.reshape(X.shape[1],1), db

# 测试
a,b,c,d = logistic(X = dating_train[['like','attr']], y = dating_train['dec'] ,w = np.zeros((2,1)) ,b = 0)
c,d

(array([[-0.05731876],
        [-0.05567185]]), 0.06749268893335386)

迭代梯度下降

输入：训练集df，y_label，学习率、迭代次数
输出：迭代过程print出来，yhat/cost/更新后的参数

def logistic_train(X, y, alpha, epochs):
    # 首先参数初始化
    n = X.shape[0]
    p = X.shape[1]
    w = np.zeros((p, 1))
    b = 0
    cost_list = []           # 记录下cost函数的递减过程
    
    # 循环迭代
    for i in range(epochs):
        yhat, cost, dw, db = logistic(X, y, w, b)   # 计算梯度
        w = w - alpha * dw      # 更新参数
        b = b - alpha * db
        cost_list.append(cost)      # 记录下cost函数的递减过程
        
        # 打印训练过程 ，每迭代100次打印一次
        if i % 100 == 0: 
            print("迭代次数:%d,  交叉熵cost=%f" % (i+1, cost))
    
    # 输出最后参数
    params = {
        'W': w,
        'b': b
    }
    grads = {
        'dW':dw,
        'db':db
    }
    print("%d次迭代结束！最终训练集上cost:%f" % (i+1, cost))
    #print(params,grads)
    return cost_list, params,yhat

# 测试
costlist, Wb, yhat = logistic_train(dating_train[['like','attr']], dating_train['dec'], 0.1, 3000)

迭代次数:1,  交叉熵cost=0.693033
迭代次数:101,  交叉熵cost=0.681541
迭代次数:201,  交叉熵cost=0.630818
迭代次数:301,  交叉熵cost=0.589915
迭代次数:401,  交叉熵cost=0.567970
迭代次数:501,  交叉熵cost=0.554228
迭代次数:601,  交叉熵cost=0.543767
迭代次数:701,  交叉熵cost=0.535549
迭代次数:801,  交叉熵cost=0.528856
迭代次数:901,  交叉熵cost=0.523552
迭代次数:1001,  交叉熵cost=0.519121
迭代次数:1101,  交叉熵cost=0.515412
迭代次数:1201,  交叉熵cost=0.512466
迭代次数:1301,  交叉熵cost=0.509890
迭代次数:1401,  交叉熵cost=0.507618
迭代次数:1501,  交叉熵cost=0.505904
迭代次数:1601,  交叉熵cost=0.504247
迭代次数:1701,  交叉熵cost=0.502922
迭代次数:1801,  交叉熵cost=0.501747
迭代次数:1901,  交叉熵cost=0.500701
迭代次数:2001,  交叉熵cost=0.499921
迭代次数:2101,  交叉熵cost=0.499082
迭代次数:2201,  交叉熵cost=0.498482
迭代次数:2301,  交叉熵cost=0.497800
迭代次数:2401,  交叉熵cost=0.497337
迭代次数:2501,  交叉熵cost=0.496777
迭代次数:2601,  交叉熵cost=0.496421
迭代次数:2701,  交叉熵cost=0.496109
迭代次数:2801,  交叉熵cost=0.495837
迭代次数:2901,  交叉熵cost=0.495446
3000次迭代结束！最终训练集上cost:0.495245

查看训练集的结果

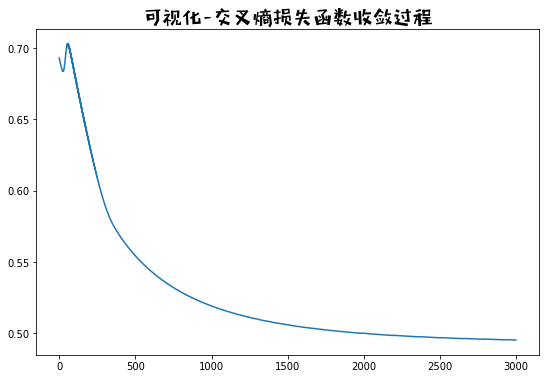
# 训练过程cost的下降过程
fig = plt.figure(figsize=(9,6))   # 创建一张8*6的画布
plt.plot(range(3000), costlist)
plt.title("可视化-交叉熵损失函数收敛过程", fontproperties=prop, fontsize=20)
plt.show() 
plt.close()

# 查看训练结果——拟合的混淆矩阵：
# 加载库画混淆矩阵
from sklearn.metrics import confusion_matrix
import seaborn as sns

# 定义预测归类函数
def pred(x, threshold=0.5):
    if x>threshold:
        return 1
    else:
        return 0

# 混淆矩阵
y_train = [pred(x) for x in yhat]
confusion_matrix(dating_train['dec'],y_train)

array([[3022,  665],
       [ 893, 1917]])

在测试集上的表现

从以下角度出发

根据参数计算yhat
pred(yhat)，比如分类阈值是0.5的时候的混淆矩阵
绘制roc曲线
可视化分类界限

# 1.计算预测集上yhat
test_yhat =  np.squeeze(sigmoid(np.dot(dating_test[['like','attr']], Wb['W']) + Wb['b']))

# 2.预测集上的混淆矩阵
y_test_pred = [pred(x) for x in test_yhat]  # 按0.5作为阈值
confusion_matrix(dating_test['dec'],y_test_pred)/dating_test.shape[0]

array([[0.47446154, 0.10461538],
       [0.14461538, 0.27630769]])

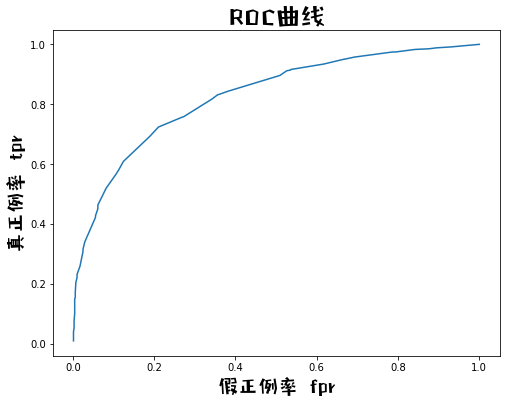
绘制roc曲线的函数（二分类问题）

######## 绘制roc曲线的函数（二分类问题） ######
# 3.roc曲线

def plot_roc(y,yhat):
    
    # 第一步、计算fpr tpr
    tpr = []
    fpr = []
    yhat_ = np.random.choice(yhat, int(len(yhat)*0.2), replace= False).tolist()   # 从样本预测值里面抽取一些
    yhat_.sort()   # 把样本预测值从小到大排序
    for i in yhat_:
        ypred = [pred(x, threshold=i) for x in yhat]   # 把抽取的预测值当做分类阈值
        cm = confusion_matrix(y,ypred)                  # 计算混淆矩阵，方便算fpr tpr
        tpr.append(cm[0,0]/(cm[0,0]+cm[0,1]))        # 真 正例率
        fpr.append(cm[1,0]/(cm[1,0]+cm[1,1]))          # 假 正例率
    
    # 第二步、画图
    fig = plt.figure(figsize=(8,6))   # 创建一张8*6的画布
    plt.plot(fpr, tpr)
    plt.title("ROC曲线", fontproperties=prop, fontsize=25)
    plt.xlabel("假正例率  fpr", fontproperties=prop, fontsize=20)
    plt.ylabel("真正例率  tpr", fontproperties=prop, fontsize=20)
    plt.show() 
    # AUC值或许可以用模拟方法求，后面可以查下资料    

plot_roc(dating_test['dec'], test_yhat)

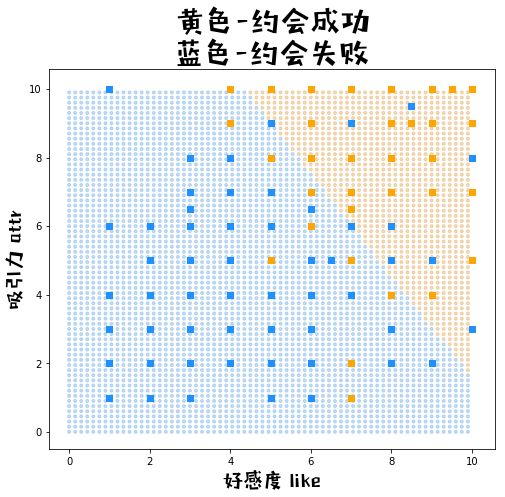
二元可视化分类界限

# 1.生成网格点数据
xx1, xx2 = np.meshgrid(np.arange(0, 10, 0.15), np.arange(0, 10, 0.15))   # 生成自变量的数据
xx = pd.DataFrame({'x1':xx1.ravel(),'x2':xx2.ravel()})                              # 拉直后合并为df
yy_hat =  np.squeeze(sigmoid(np.dot(xx, Wb['W']) + Wb['b']))                # 预测
yy_pred_ = [pred(x) for x in yy_hat]                                    # 按0.5作为阈值对预测值分类  
yy_pred = np.array(yy_pred_).reshape(xx1.shape)                  # reshape为网格/矩阵

# 2.画图
fig = plt.figure(figsize=(8,7))   # 创建一张8*6的画布
# 2.1背景网格点
color = ["#e2a653" if c==1 else "#6cabe6" for c in yy_pred_] 
plt.scatter(xx1, xx2, c = color, alpha = 0.4, marker= ".")

# 2.2原始数据的点
color = ["orange" if c==1 else "dodgerblue" for c in dating_test['dec']] 
plt.scatter(dating_test['like'],dating_test['attr'], c=color, marker= "s")

# 3.图例
plt.title('黄色-约会成功\n蓝色-约会失败', fontproperties=prop, fontsize=30)  
plt.xlabel("好感度 like", fontproperties=prop, fontsize=20)
plt.ylabel("吸引力 attr", fontproperties=prop, fontsize=20)

手动实现——Logistic与Roc曲线

思路：

数据预处理

定义函数——计算交叉熵的cost&梯度

迭代梯度下降

查看训练集的结果

在测试集上的表现

绘制roc曲线的函数（二分类问题）

二元可视化分类界限

感谢您的支持，我会继续努力的!