kmeans

思路

1. 随机选择初始k个样本点
2. 对每个非中心样本点计算到k个中心点的距离，归入距离最小的一类
3. 重新计算中心，重复第二步

停止条件：迭代停止条件/中心点不变

## 导入模块
import numpy as np
import matplotlib.pyplot as plt

## 将代码块运行结果全部输出，而不是只输出最后的，适用于全文
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"    

## 生成数据
X = np.array([[1.5, 5], [2, 7.5],[2.3, 3.9], [2,3.1], [2.5, 6], [3, 5.7], [3.3, 2.9], [4, 8], [4,6.6],
              [6, -1], [5, 0.5], [5.5, 3.9], [6,2], [6.4,1.2],[7,-0.5], [6.7, 3], [7.5, 0.5]])
x1 = [x[0] for x in X]
x2 = [x[1] for x in X]
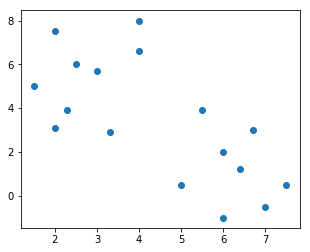
fig = plt.figure(figsize = (5, 4))   # 创建一张画布
plt.scatter(x1, x2)

# 1.定义函数——抽取初始值
import random
def sample(data, sample_size):
    sample_list = []
    number_set = list(range(X.shape[0]))
    for i in range(sample_size):  # 独立抽样
        num = random.choice(number_set)
        number_set.remove(num)   # 不放回
        sample_list.append(num)
    return sample_list


# 2.定义函数——对于非中心点归类
def cluster(X, centriod):
    new_cluster = []
    number_list =  list(range(X.shape[0]))
    for i in number_list:
        closest_dist = float('inf')
        closest_i = None
        for j in range(len(centriod)):
            l2_dist = np.dot((centriod[j] - X[i]).T, centriod[j] - X[i])
            if l2_dist < closest_dist:
                closest_dist = l2_dist
                closest_i = j
        new_cluster.append(closest_i) 
    return new_cluster


# 3.定义函数——更新中心点
def new_centriod(X, new_cluster):
    cluster1 = []
    cluster2 = []
    number_list =  list(range(X.shape[0]))
    for i in number_list:
        if new_cluster[i] == new_cluster[0]:
            cluster1.append(X[i])
        else:
            cluster2.append(X[i])
    new_k  = [np.mean(cluster1, axis = 0), np.mean(cluster2, axis = 0)]
    return new_k

inital_k = sample(list(range(X.shape[0])), 2)  # k=2 分为两类的情况
print("选取的初始中心点为:{}".format(inital_k)) # 选取的初始值
new_k = np.array([X[k] for k in inital_k])

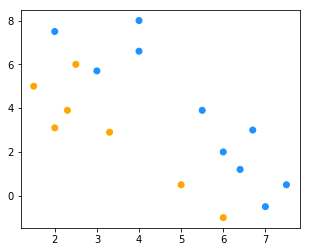
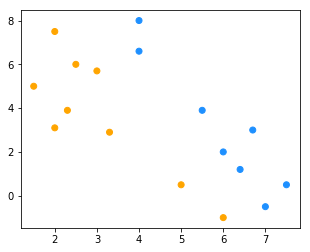
for _ in range(3):  # 多次迭代
    new_cluster = cluster(X, new_k)
    color = ["orange" if c == new_cluster[0] else "dodgerblue" for c in new_cluster] 
    fig = plt.figure(figsize=(5, 4))    # 创建一张画布
    plt.scatter(x1, x2, c = color)
    new_k = new_centriod(X, new_cluster)

选取的初始中心点为:[8, 0]

inital_k = sample(list(range(X.shape[0])), 2)  # k=2 分为两类的情况
print("选取的初始中心点为:{}".format(inital_k)) # 选取的初始值
new_k = np.array([X[k] for k in inital_k])

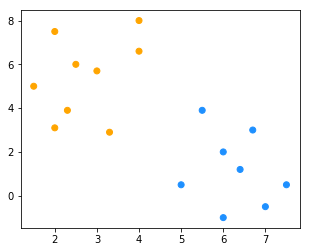
for _ in range(3):  # 多次迭代
    new_cluster = cluster(X, new_k)
    color = ["orange" if c == new_cluster[0] else "dodgerblue" for c in new_cluster] 
    fig = plt.figure(figsize=(5, 4))    # 创建一张画布
    plt.scatter(x1, x2, c = color)
    new_k = new_centriod(X, new_cluster)

选取的初始中心点为:[10, 15]

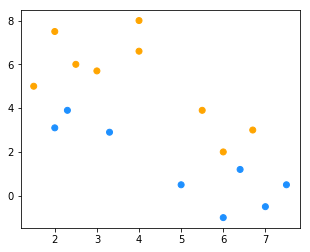
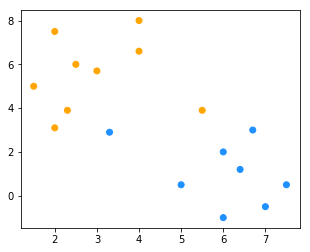
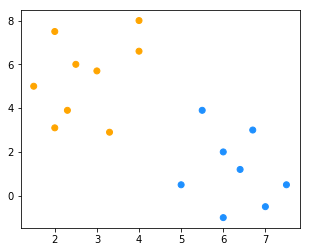
【小总结】分类过程和结果都依赖于初始值的选择