主要内容：隐变量、EM算法的引入、一般流程、高斯混合模型的EM算法、Kmeans与EM算法关系、EM算法的推出。首先声明，本文来源于我个人理解，可能有误欢迎纠错嗷！至于写这篇的原因，只是希望通过梳理自己学到的，或许尝试输出才知道哪里没有理解。

引入EM算法

一个简单的例子

现在有2个袋子，里面都装着红球和白球。第一步随机选择一个袋子，第二步从选出的袋子里取出一个球，记录取出的球的颜色。

1. 假设我们知道所有的参数

假设我们知道第一步中随机选到1号袋子的概率是 $\pi$ ，选到二号袋子的概率是 $1-\pi$ ，并且我们知道每个袋子里面红球和白球的比例为：

-	1号袋子	二号袋子
红球	p	1-p
白球	q	1-q

那么我们可以根据参数计算出许多概率/条件概率，比如已知第二步取到白色球，想问它属于1号袋子的条件概率是多少？由贝叶斯公式可知：

p(1 | white) = \frac{p(white|1)p(1)}{p(white|1)p(1) + p(white|2)p(2)}

2. 假设我们不知道所有参数

现在我们想要估计所有的参数 $\theta = {\pi, p, q}$ （待估、未知的），定义隐变量：表示第一步我们随机抽取的袋子是1号袋子还是2号袋子（是不可观测的），定义观测变量：表示最后我们取出的是红球还是白球（可观测的）。从极大似然估计的角度出发怎么解决呢？假设试验独立重复n次，则似然函数为:

$\Pi_{i} p(y_i|\theta)$ (全概率公式展开) = $\Pi_{i} \Sigma_{z} p(y_i, z | \theta) p(z|\theta)$ = $\Pi_{i} [\pi p^{y_i} (1-p)^{y_i} + (1-\pi) q^{1- y_i} (1-q)^{1- y_i} ]$

参数的极大似然估计值为 = $\arg\max\limits_{\theta} \Sigma_{i} log(p(y_i|\theta))$

3. 鸡生蛋蛋生鸡问题

针对这种包含隐变量的参数估计问题，我们想要解决的问题其实是“鸡生蛋蛋生鸡”的相互依赖问题

问题一，我们想要估计参数，首先要确定每个球到底来自哪个袋子（即确定隐变量的取值）才能写出似然函数的表达式
问题二，隐变量是不可观测的，需要根据参数和观测变量来判断 Z 的取值概率（什么意思呢？比如1号袋子红球多而2号袋子白球多，当我们取到白球时可以认为该球来自2号袋子，或者说“Z=2号袋子”的概率更大）

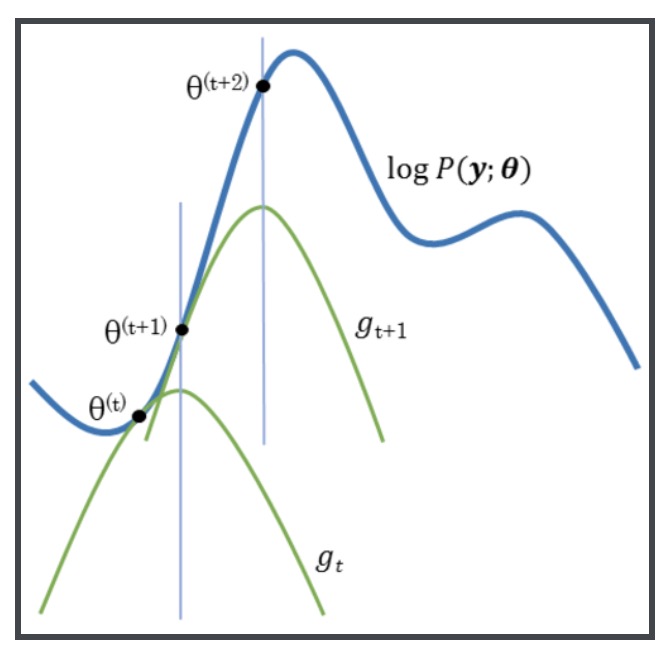
EM算法的求解思想认为：两个问题相互依赖，转化为一个动态求解过程。随机化给定参数 $\theta$ 初始值，根据参数初始值可以算出每个样本来自1号或者2号袋子的条件概率（E步），然后据此用极大似然调整参数估计值（M步），见下图所示。

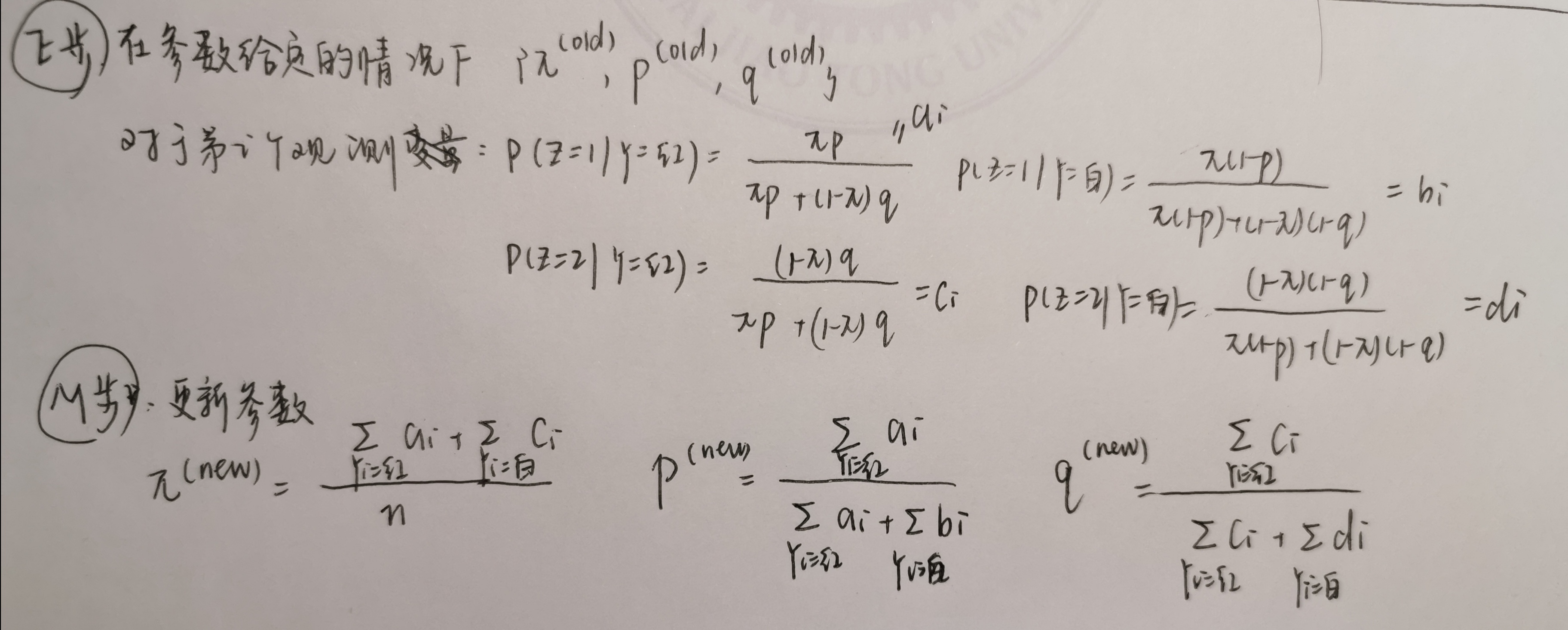
通过不断动态迭代调整，直到满足终止条件，输出参数估计（局部最优值）

4. 取红球问题的模拟

假设取到一号袋子的概率是0.4，取到二号袋子的概率是0.6，一号袋子里红球比例为0.6，二号袋子里红球比例为0.4。

import numpy as np

# 初始化参数
pi = 0.8; p = 0.2; q = 0.9;n = 200
theta_true = np.array([pi, p, q])
thetas = np.array([0.8 ,0.9, 0.5])

for i in range(5):
    # 1.生成观测数据
    observed_y = []
    for _ in range(n):
        bags = np.random.binomial(1, theta_true[0])
        yi= np.random.binomial(1, theta_true[1]) if bags else np.random.binomial(1, theta_true[2])
        observed_y.append(yi)
    observed_y = np.array(observed_y)

    # E步
    ai = observed_y * (thetas[0] *  thetas[1])  / (thetas[0] *  thetas[1] + (1- thetas[0]) * thetas[2] )
    ci = observed_y * (1- thetas[0]) * thetas[2] / (thetas[0] *  thetas[1] + (1- thetas[0]) * thetas[2] )
    bi = (1 - observed_y) * (thetas[0] *  (1- thetas[1])) /  (thetas[0] * (1- thetas[1]) + (1 - thetas[0] ) * (1- thetas[2]))
    di = (1 - observed_y) * ((1 - thetas[0] ) * (1- thetas[2])) /  (thetas[0] * (1- thetas[1]) + (1 - thetas[0] ) * (1- thetas[2]))
    # M步
    pi_new = np.mean(ai + bi) 
    p_new = np.sum(ai)  / np.sum(ai + bi)
    q_new = np.sum(ci)  / np.sum(ci + di)
    thetas = np.array([pi_new, p_new, q_new])
    # print
    print("times: %d" % ( i +1))
    print("π = %.3f, p = %.2f, q = %.2f" 
                  % (thetas[0], thetas[1], thetas[2]))

times: 1
π = 0.564, p = 0.43, q = 0.08
times: 2
π = 0.588, p = 0.49, q = 0.10
times: 3
π = 0.603, p = 0.53, q = 0.11
times: 4
π = 0.590, p = 0.50, q = 0.10
times: 5
π = 0.598, p = 0.52, q = 0.11

看起来结果不是很ok？如何验证呢，由大数定律可知应该有 $\pi p + (1-\pi) q = \frac{k}{n}$ （观测数据中红球的比例）,最终只要我们的三个参数满足这一个方程就是合理的，可见解不唯一，主要原因是参数数>方程的个数，当数据更高维时就不一定是这样了。

print(theta_true[0] * theta_true[1] + (1-theta_true[0]) * theta_true[2],  thetas[0] * thetas[1] + (1-thetas[0]) * thetas[2])

0.3499999997 0.355

why EM算法

通常情况下我们对似然函数或者对数似然求偏导，然后求出偏导=0且二阶导<0的极值点。然而由于隐变量的存在，我们发现这个问题复杂了起来，变成了一个非凸问题，没有全局最优解析解。

如何求解一个非凸问题？梯度下降、EM算法等等来求出局部最优解

梯度下降 v.s. EM算法

梯度下降时是通用方法
EM算法不用调参收敛代码简单但只适用于部分非凸问题

算法内容

算法的一般流程

高斯混合模型下EM算法的流程

高斯混合模型的参数估计是EM算法的一个重要应用。下面看起来很长，其实是根据EM算法一般流程进行“公式套用”哈~ 主要步骤为：

写出对数似然函数
E步求期望，利用全概率公式，得到隐变量取值的条件概率
M步，带入E步的值，再极大化对数似然函数，更新参数估计值（其实就是对参数求极大似然估计）

K均值与EM算法的关系

联系
K均值算法其实利用了EM算法的思想，E步时把每个点归入某类，M步时候重新计算类中心点。
区别：
EM算法的E步中，我们用上一次参数迭代值和观测值，求出观测样本的隐变量取值的条件概率。注意！我们不是每个点归入某个总体，而是给出它来自某个总体的概率值，这个概率值在0-1之间，这就做软分配。
而 k-means 不同于此，它把每个点直接归入某类。求隐变量取值的条件概率时候，先找出某个观测点与各中心点距离最小的那一类，直接令属于这一类概率=1，其他类=0，而不是以一定概率来自某类，这就叫做硬分配。

似然函数下界的推导

心塞之前看完立马忘光光，现在只能看着笔记本发愣，感觉有一步奇奇怪怪（裂开）

蛮奇怪的一点，就是如何理解EM算法通过提升下界，使得对数似然函数不断提升的。下面这张图或许可以说明白：

EM算法